LCT——优雅但玄学的动态树

建议在右侧的设置按钮中打开阅读器模式阅读

虽然基于 Splay，但是并没有 Splay 难调

LCT 简介

LCT 是一种解决动态树问题的算法，就是在树链剖分的基础上可以断开或连接边（当然保证还是一棵树）。

那么对于这种问题，自然就不能用重链剖分来解决，这时便需要一个新的组合——实链剖分+Splay

模板题看这里

实链剖分

对于一个点连向它所有儿子的边，我们自己选择一条边进行剖分，我们称被选择的边为实边，其他边则为虚边。对于实边，我们称它所连接的儿子为实儿子。对于一条由实边组成的链，我们同样称之为实链 —— Oi-Wiki

Splay

先放两篇博客，毕竟这种被 FHQ 吊打的数据结构不太想写，也只需要会一点点就好了

「学习笔记」平衡树——splay 一

「学习笔记」平衡树——splay 二

算法讲解

思路

对于一棵树，我们将它剖成若干条实链：

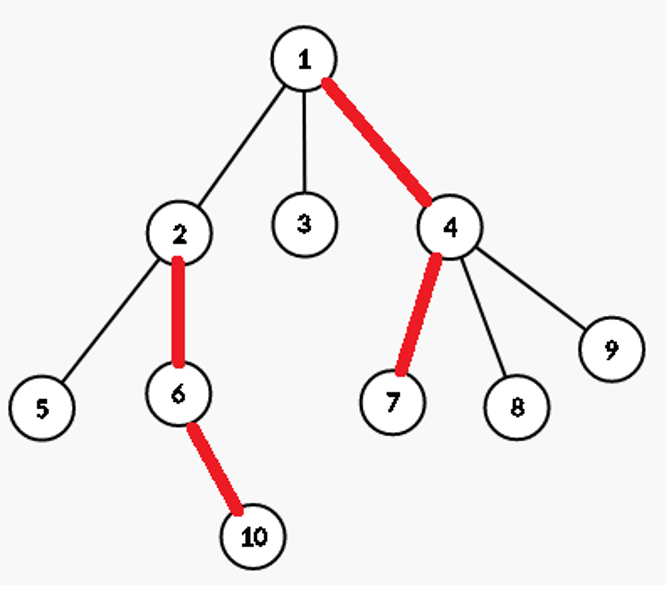
如图所示，整棵树被剖分成{1,4,7},{2,6,10},{3},{5},{8},{9}这些实链。

所以我们可以以深度为关键字，对每条连用一棵 Splay 来维护。

但是我们如何对于原树进行维护？可以对每一棵 Splay 的链顶的父亲节点进行记录，但是从原树上的父亲不会向它连边

具体实现可以将链顶的 fa 值设为链头在原树上的父节点

然后就可以用一棵新的树，也就是辅助树替代掉原树：

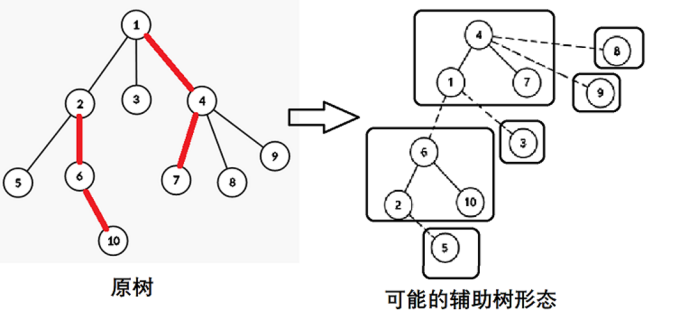
这就是 LCT 大致的思路。

实现

先鸽一下……

本人用的结构体写法……

Splay 部分

结构体：

struct node
{
    int val, xval;//每个结点的值，Splay上子树异或和
    int ch[2], fa, lazy_rev;//子节点，父节点，翻转的懒标记
} tr[N];

上传与下放：

void pushup(int x)
{
    tr[x].xval = tr[tr[x].ch[0]].xval ^ tr[tr[x].ch[1]].xval ^ tr[x].val;
}
void pushdown(int x)
{
    if(tr[x].lazy_rev)
    {
        int p;
        if(p = tr[x].ch[0]) swap(tr[p].ch[0], tr[p].ch[1]), tr[p].lazy_rev ^= 1;
        if(p = tr[x].ch[1]) swap(tr[p].ch[0], tr[p].ch[1]), tr[p].lazy_rev ^= 1;
    }
    tr[x].lazy_rev = 0;
}
//不过多解释

旋转：

void rotate(int x)
{
    int y = tr[x].fa, z = tr[y].fa, k = getch(x);
    if(!isroot(y)) tr[z].ch[getch(y)] = x; tr[x].fa = z;//1
    tr[y].ch[k] = tr[x].ch[k ^ 1]; tr[tr[y].ch[k]].fa = y;
    tr[x].ch[k ^ 1] = y, tr[y].fa = x; pushup(y);
}
//这里与Splay并没有本质上的区别，只是1处需要判断以保障不会影响到别的树，isroot(z)在下文

伸展：

void splay(int x)
{
    update(x);
    while(!isroot(x))
    {
        if(!isroot(tr[x].fa)) rotate(getch(x) ^ getch(tr[x].fa) ? x : tr[x].fa);
        rotate(x);
    }
    pushup(x);
}
//这里与Splay并没有本质上的区别，只是判断旋转到顶使用isroot(x)

LCT 部分

一共十个函数……
判断是哪棵子树:

int getch(int x)
{
    return tr[tr[x].fa].ch[1] == x;
}

判断是否为根:

bool isroot(int x)
{
    return tr[tr[x].fa].ch[0] != x && tr[tr[x].fa]. ch[1] != x;
    //由于根节点连出后所指的fa并不会认它为子结点，便可以以此判断
}

操作从根到x上的所有子节点的懒标记:

void update(int x)
{
    if(!isroot(x)) update(tr[x].fa);//递归处理
    pushdown(x);
}
//在执行splay(x)之前，由于树的形态会改变，因此要清空懒标记

下面是整个 LCT 中最核心的操作——将 x 到根打通为实链（仅是从 x 到根路径上的点）

对于在 x 点时，显然不会有实链，所以将 x 伸展到根后直接断开 x 与下面的连接

在其他点时，伸展到根后两部分：左儿子——在当前链上深度小于当前点的部分，右儿子——在当前链上深度大于当前点的部分。那么因为要把当前点与上一次的连接，就断开与右儿子的连接，将上一次操作的点连在右儿子上。

一直这样操作直到连到原树树根。

void access(int x)
{
    int p = 0;
    for(; x; p = x, x = tr[x].fa)
    {
        splay(x);
        tr[x].ch[1] = p;
        pushup(x);
    }
}

将x换为原树的根：

void makeroot(int x)
{
    access(x);//打通x到根节点
    splay(x);//将x伸展到根
    swap(tr[x].ch[0], tr[x].ch[1]);//将这条链的Splay翻转
    tr[x].lazy_rev ^= 1;
}

将x~y打通成实链:

int split(int x, int y)
{
    makeroot(x);//将x变为原树的根
    access(y);//打通y与原树的根（就是x）
    splay(y);//将y伸展到Splay的根（为了均摊复杂度与后续操作）
    return y;
}

找x所在原树的根:

int find(int x)
{
    access(x);//打通x到根节点
    splay(x);//将x伸展到根
    //下面是找子树中最左的
    pushdown(x);
    while(tr[x].ch[0])
    {
        x = tr[x].ch[0];//向左跳
        pushdown(x);//下放
    }
    splay(x);//将x伸展到Splay的根（为了均摊复杂度）
    return x;
}

连接x，y点:

void link(int x, int y)
{
    makeroot(x);//将x作为树根
    if(find(y) != x) tr[x].fa = y;//如果x，y不在一棵树，连接
}

断开x, y:

void cut(int x, int y)
{
    split(x, y);//打通x，y
    if(tr[y].ch[0] == x && tr[x].ch[1] == 0)、
    /*
        此时y在split中变成了Splay的根节点
        x，y深度仅会相差1
        当此时y是Splay的根，x是深度最低的树根
        则x必须是y的左儿子且x没有右儿子
    */
    {
        tr[y].ch[0] = tr[x].fa = 0;//断开
        pushup(y);
    }
}

修改x的点权：

void fix(int x, int v)
{
    splay(x);//将x伸展到Splay的根，方便操作
    tr[x].val = v;//修改x的值
    pushup(x);
}

完整代码

70行极限压行，真男人才懂得压行的魅力~

//problem: P3690 【模板】动态树（LCT）
//date: 2023.11.23-5:00
#include <bits/stdc++.h>
#define int long long
#define FH signed
using namespace std;
const int N = 1e5 + 10;
struct node {int val, xval, ch[2], fa, lazy_rev;} tr[N];
int getch(int x) {return tr[tr[x].fa].ch[1] == x;}
void pushup(int x) {tr[x].xval = tr[tr[x].ch[0]].xval ^ tr[tr[x].ch[1]].xval ^ tr[x].val;}
void pushdown(int x)
{
    if(tr[x].lazy_rev)
    {
        int p;
        if(p = tr[x].ch[0]) swap(tr[p].ch[0], tr[p].ch[1]), tr[p].lazy_rev ^= 1;
        if(p = tr[x].ch[1]) swap(tr[p].ch[0], tr[p].ch[1]), tr[p].lazy_rev ^= 1;
    }tr[x].lazy_rev = 0;
}
bool isroot(int x) {return tr[tr[x].fa].ch[0] != x && tr[tr[x].fa]. ch[1] != x;}
void update(int x) { if(!isroot(x)) update(tr[x].fa); pushdown(x);}
void rotate(int x)
{
    int y = tr[x].fa, z = tr[y].fa, k = getch(x);
    if(!isroot(y)) tr[z].ch[getch(y)] = x; tr[x].fa = z;
    tr[y].ch[k] = tr[x].ch[k ^ 1]; tr[tr[y].ch[k]].fa = y;
    tr[x].ch[k ^ 1] = y, tr[y].fa = x; pushup(y);
}
void splay(int x)
{
    update(x);
    while(!isroot(x)) {if(!isroot(tr[x].fa)) rotate(getch(x) ^ getch(tr[x].fa) ? x : tr[x].fa); rotate(x);}
    pushup(x);
}
void access(int x)
{
    for(int p = 0; x; p = x, x = tr[x].fa)
        splay(x), tr[x].ch[1] = p, pushup(x);
}
void makeroot(int x) {access(x), splay(x), swap(tr[x].ch[0], tr[x].ch[1]), tr[x].lazy_rev ^= 1;}
int split(int x, int y) {makeroot(x), access(y) , splay(y); return y;}
int find(int x)
{
    access(x), splay(x), pushdown(x);
    while(tr[x].ch[0]) x = tr[x].ch[0], pushdown(x); splay(x);
    return x;
}
void link(int x, int y) {makeroot(x); if(find(y) != x) tr[x].fa = y;}
void cut(int x, int y) {split(x, y); if(tr[y].ch[0] == x && tr[x].ch[1] == 0) tr[y].ch[0] = tr[x].fa = 0, pushup(y);}
void fix(int x, int v) {splay(x), tr[x].val = v, pushup(x);}

FH main()
{
    // ios::sync_with_stdio(0);
    // cin.tie(0);
    // cout.tie(0);
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> tr[i].val;
    for(int i = 1; i <= m; i ++)
    {   
        int opt, x, y;
        cin >> opt >> x >> y;
        if(opt == 0) cout << tr[split(x, y)].xval << "\n";
        if(opt == 1) link(x, y);
        if(opt == 2) cut(x, y);
        if(opt == 3) fix(x, y);
    }
    return 0;
}//FH

说句闲话，这是我生日过的紫题呢~~~

完结撒花~~~