0x00 引入
给定主串与模式串 ,问主串中是否存在模式串。
实际上这是一个最为简单的字符串匹配问题,对于暴力匹配来讲,每一次匹配失败时将模式串后移一位从头开始匹配是 O ( n 2 ) O(n^2) O ( n 2 )
而观察会发现,上述的解法会有很多次不必要的匹配过程,而 KMP 则可以减少匹配次数,Z 函数则是用另外的方法对更多信息进行处理,经过适当转换也可解决上述问题。
0x01 KMP
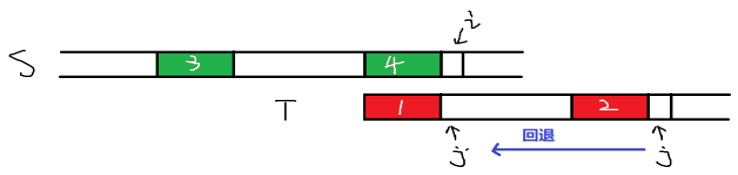
对与上图的情况,我们假设 1、2、3、4 部分是一样的,那么我们在 j j j t j ≠ s i t_j \ne s_i t j = s i j j j j ′ j' j ′
假如我们已经知道了在每个点应回退到那个位置,即 nxt[] 数组,不难写出以下代码:
1 2 3 4 5 6 7 8 9 10 void kmp(string s, string t) { int n = s.size(), m = t.size(); for(int i = 0, j = 0; i < n; i ++) { while(j > 0 && s[i] != t[j]) j = nxt[j - 1]; if(s[i] == t[j]) j ++; if(j == m) cout << i + 1 - m + 1 << "\n";//这是输出在哪个位置出现了模式串,具体题目具体分析 } }
回到最麻烦的问题,如何知道该回退到哪一个地方?
考虑一点,由于下标从 0 0 0 nxt[i] 存的值是在模式串从 到 组成的字符串中,最长的公共前后缀(特别的,此处不能是整个串)的长度。
那么为了线性的复杂度,我们需要想办法利用 nxt[j-1] 的值对 nxt[j] 进行计算。
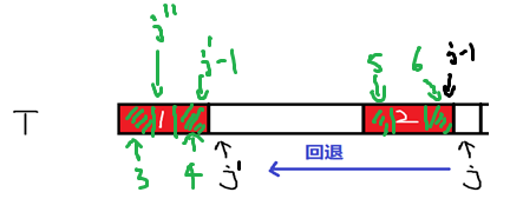
对于上图,j ′ = n x t j − 1 , j ′ ′ = n x t j ′ − 1 j'=nxt_{j-1},j''=nxt_{j'-1} j ′ = n x t j − 1 , j ′′ = n x t j ′ − 1 t j ≠ t j ′ t_j\ne t_{j'} t j = t j ′ t j ′ ′ t_{j''} t j ′′ t j t_j t j 实在只能讲成这样了,感性理解一下吧
代码就好写了~~
1 2 3 4 5 6 7 8 9 10 11 void init(string t) { int m = t.size(); nxt[0] = 0; for(int i = 1, j = 0; i < m; i ++) { while(j > 0 && t[i] != t[j]) j = nxt[j - 1]; if(t[i] == t[j]) j ++; nxt[i] = j; } }
0x02 Z 函数(扩展KMP)
鸽一下
不鸽了(
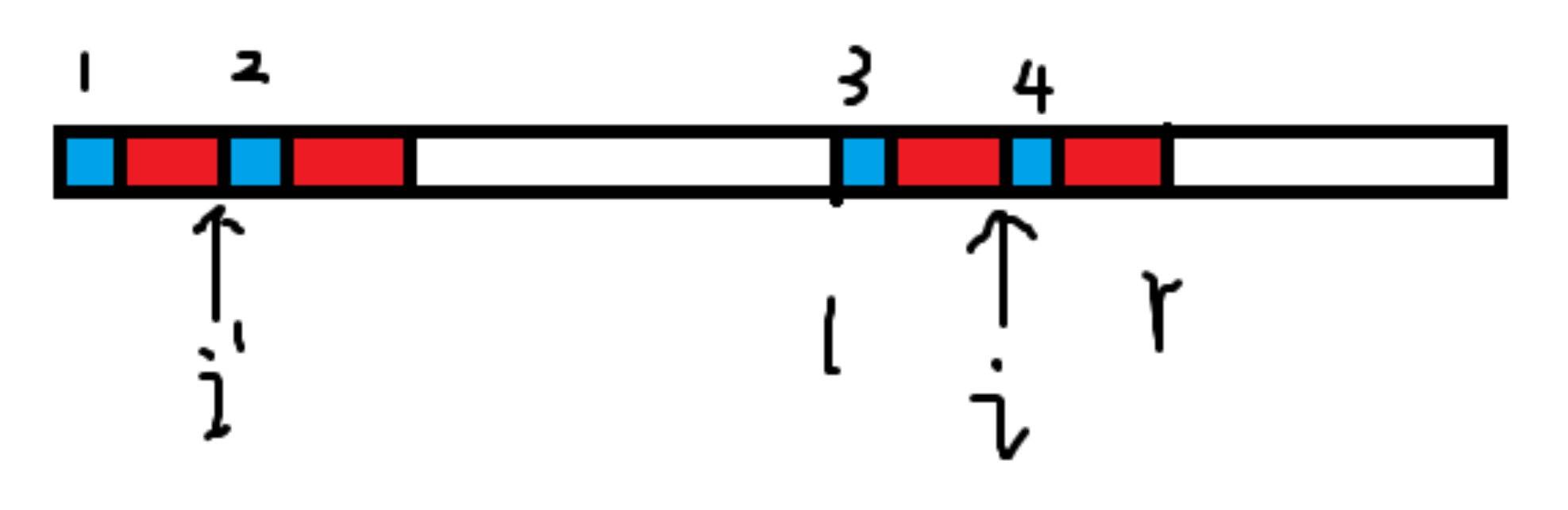
对于 s s s s i s_i s i z i z_i z i s s s z 0 = 0 z_0=0 z 0 = 0
我们可以定义一个 Z-box,表示已知的右端点最靠右的 LCP,记该区间为 [ l , r ] [l,r] [ l , r ]
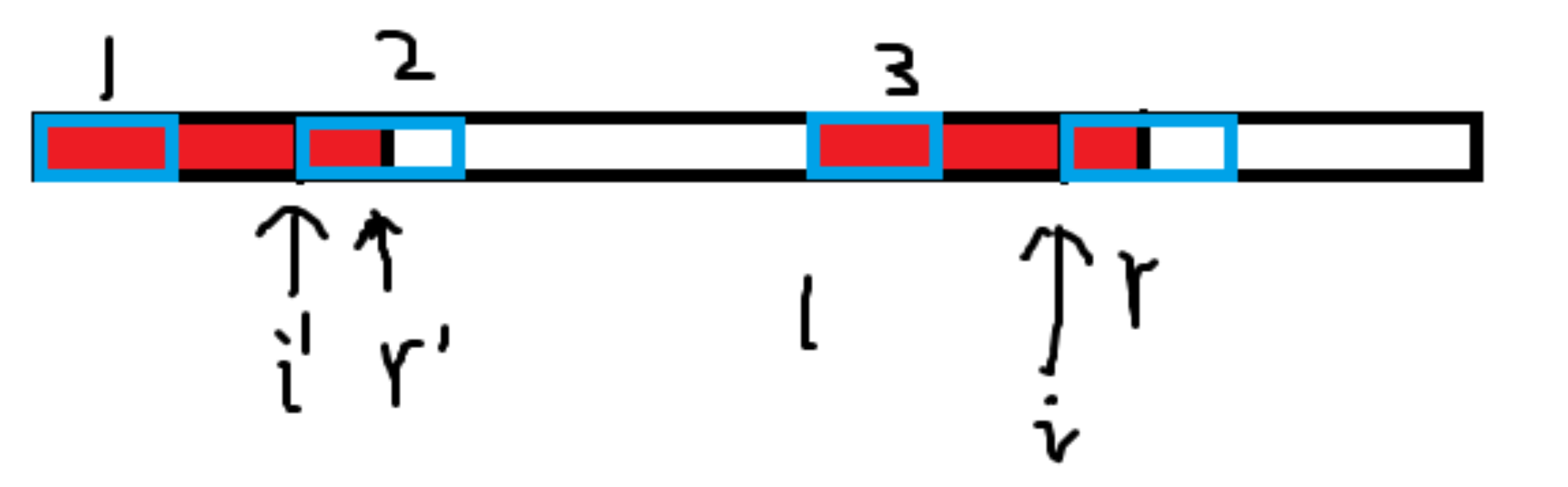
那么就会有下面两种情况:
i ′ + z i ′ < r i' + z_{i'} < r i ′ + z i ′ < r z i z_i z i z i ′ z_{i'} z i ′
i ′ + z i ′ ≥ r i' + z_{i'} \ge r i ′ + z i ′ ≥ r
至于实现字符串匹配,将模式串加上分隔符与主串拼接,若 z i = ∣ 模式串长度 ∣ z_i=|\text{模式串长度}| z i = ∣ 模式串长度 ∣
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void z_algorithm (string s, int z[]) int l = 0 , r = 0 , n = s.size (); z[0 ] = 0 ; for (int i = 1 ; i < n; i ++) { if (i <= r && z[i - l] < r - i + 1 ) z[i] = z[i - l]; else { z[i] = max (0LL , r - i + 1 ); while (i + z[i] < n && s[i + z[i]] == s[z[i]]) z[i] ++; } if (i + z[i] - 1 > r) l = i, r = i + z[i] - 1 ; } }
完结撒花~~~